 |
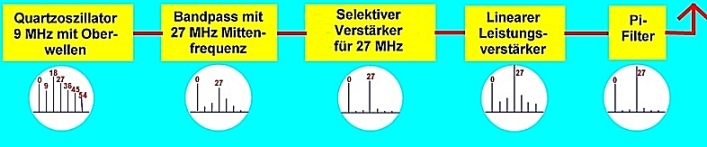
| Abb.1: Synthese durch selektives Ausfiltern eines oberwellenreichen Quartzsignals |
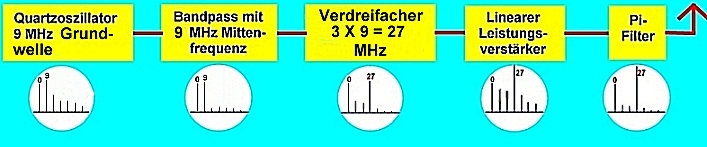 |
| Abb.2: Synthese durch Frequenzverfielfachung einer Grundwellenschwingung |
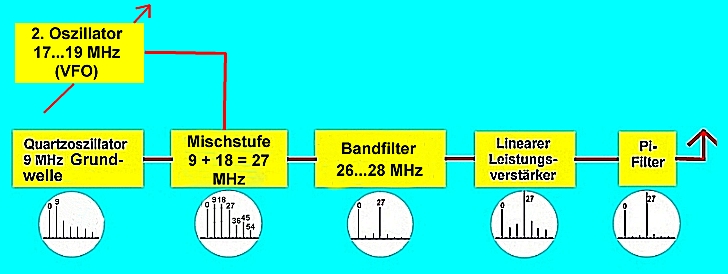 |
| Abb.3: Synthese durch Mischung eines Quartzsignals mit einer variablen Frequenz |
Oberwellen 3
Um nun aus einer vorhandenen, oberwellenreichen Grundschwingung ein brauchbares und stabiles Sendesignal zu erhalten, wird man zunächst diese Grundschwingung durch Auswahl spezieller Oszillatorenschaltungen, zusätzlicher Quartzstabilisierung und verschiedenen Maßnahmen zur Temperaturkompensation schon von vorneherein so stabil wie möglich generieren.
Die nachfolgenden Stufen der Aufbereitung beinhalten verschiedene Möglichkeiten:
Entweder man filtert einfach die gewünschte Oberwelle aus und verstärkt diese dann linear in Transistor oder Röhrenstufen bis auf die gewünschte Ausgangsleistung nach, oder man verwendet das Prinzip der Frequenzmischung:
Wohl jeder kennt den Effekt des Schwebungstones, wie er etwa beim Stimmen einer Gitarre auftritt: Hierbei werden zwei unterschiedliche Frequenzen (Die der Gitarrenseite und die einer Stimmgabel, oder eines Pfeifchens, oder auch einer anderen Gitarrenseite) mit dem Ohr verglichen und auf sogenanntes "Schwebungsnull" abgestimmt. Eine Schwebung (Überlagerung) ist nicht weiter als ein zusätzlich auftretender, und in seiner Tonhöhe von der Differenz der beiden gemischten Ausgangstöne abhängiger, dritter Ton, der beim Stimmen deutlich zusammen mit den Ausgangstönen hörbar ist. Je ähnlicher die Frequenz der Ausgangstöne untereinander ist, desto niedriger wird auch die Frequenz des resultierenden Schwebungstones sein, um bei annähernder Frequenzgleichheit der Ausgangssignale über ein sehr langsames An-und Abschwellen (Schwebung) schließlich völlig zu verschwinden.-Diesen Punkt nennt man Schwebungsnull und das Vefahren ist extrem empfindlich.
Theoretisch bilden sich beim Mischen zweier, reiner Grundschwingungen gleicher Amplitude (=Lautstärke) aber verschiedener Frequenz (F1 und F2) Schwebungsfrequenzen der Summe und Differenz ( F1 +F2, sowie F1 -F2, bei F1 >F2). Das gilt für hörbare Töne ebenso wie für Hochfrequenzschwingungen
.
Um ein Beispiel zu nennen: Mischt man etwa ein Sinussignal von 100 MHz mit einem weiteren Sinussignal von 60 Mhz, so treten sofort Mischprodukte von 100+60 = 160 Mhz, 100-60 = 40 MHz, und natürlich auch eine Unzahl weiterer Mischprodukte mit den auf diese Art entstandenen Schwebungen ( Zum Beispiel: 160+100 = 260 MHz, 40+260 = 300 MHz, 300+40 = 340 Mhz.... usw.) auf, die als Oberwellen und Subharmonische um die beiden reinen Ausgangsfrequenzen ein komplettes neues Spektrum generieren.- Man kann sich daher leicht ausrechnen was es bedeutet, wenn man von vorneherein schon statt der beiden "sauberen" Sinusschwingungen ooberwellenreichere Signale verwendet hätte.- Es bildet sich nach dem Schneeballprinzip ein unüberschaubarer Nebenwellenmatsch, quer über das gesamte Spektrum. Setzt man nun statt der diskreten Quartzfrequenz dann noch frei und somit instabil schwingende Oszillatoren ein, und moduliert möglicherweise die Anordnung zusätzlich,was einer Mischung von Hochfrequenz mit Niederfrequenz gleichkommt, driftet dieses Spektrum weitab aller geradzahligen Vielfachen auch noch über ungeradzahlige Mischungsvarianten und es resultiert daraus ein Hochfrequenzrauschen welches natürlich bestens als Störsender über alle Bänder geeignet wäre.
Um das Mischprinzip sinnvoll zu nutzen, müssen also möglichst saubere Ausgangssignale mit entsprechenden Filtern kombiniert werden, die die unerwünschten Nebenprodukte unterdrücken. Zum Mischen selbst kann man bei ausreichenden Leistungspegeln entweder simple, passive HF Übertrager (Spezielle Transformatoren) oder auch aktive, transistorisierte Mischstufen mit speziellen HF-Transistoren verwenden, wobei in beiden Fällen noch ein oder mehrere selektive Filter zur "Reinigung" des Signals nachgeschaltet werden. Die bekannteste Filterart zur Oberwellenunterdrückung besteht aus ein- oder mehrstufigen Tiefpässen und eignet sich zum Beispiel in Sendeendstufen als sogenanntes Pi-Filter zusätzlich hervorragend zur bequemen Antennenanpassung. In folgender Blockgrafik nun habe ich verschiedene Möglichkeiten der Trägerfrequenzsynthese eines Senders dargestellt:
 |
| Abb.1: Synthese durch selektives Ausfiltern eines oberwellenreichen Quartzsignals |
 |
| Abb.2: Synthese durch Frequenzverfielfachung einer Grundwellenschwingung |
 |
| Abb.3: Synthese durch Mischung eines Quartzsignals mit einer variablen Frequenz |
Natürlich sind alle diese Blockschaltungen stark vereinfacht und keineswegs vollständig, reichen aber zur Erklärung der Eigenschaften von Oberwellen und deren Nutzung vom Prinzip her völlig aus. Vielleicht werde ich bei entsprechendem Interesse meiner Besucher die Kapiteln auch noch um detailliertere Ausführungen und Schaltpläne erweitern.
Mailen Sie mich an: technodoc@technodoctor.de