Das Bändermodell und die Halbleiter

Ausgehend vom Gleichrichtereffekt des primitiven Kristalldetektors forschte man in der Festkörperphysik fieberhaft nach anderen Anordnungen und Materialien um einen Detektor zu bauen, der nicht ständig nachjustiert werden musste. Die beim Kristalldetektor benutzten Eisen- oder Kupfersulfidkristalle waren dabei ungeeignet, da ihre Halbleitereigenschaften nicht so ausgeprägt und vorausberechenbar waren, dass man damit zuverlässige Gleichrichter hätte herstellen können.- Durch genau diese Unberechenbarkeit drückten sich die Festkörperphysiker auch lange Zeit um die systematische Erforschung der Halbleiter herum, da die meisten Experimente durch verschiedene Reinheitsqualitäten der verwendeten Substanzen in ihren Ergebnissen stark differierten und somit nicht korrekt reproduzierbar waren. Ausserdem hing die Gleichrichterwirkung offenbar nicht nur ausschließlich vom verwendeten Kristall ab, sondern auch noch von Material und Position der Federspitze,die den Kristall berührte.-Verwendete man etwa einen Kupfersulfidkristall, gelang der Effekt zum Beispiel am besten mit einer Aluminiumfeder, und war bei einer Stahlfeder so gut wie nicht mehr vorhanden. Zudem handelte es sich um natürliche Kristalle mit zahlreichen Verunreinigungen und Inhomogenitäten, die sehr stark in ihren elektrischen Eigenschaften variierten. Man suchte also zunächst lange Zeit nach anderen Kristallen, die man schließlich selber in hoher Reinheit züchten konnte und entdeckte schon bald die Vorzüge von hochreinen Silizium- und Germaniumkristallen, die man in einem Stück als Kristallstab aus der Schmelze ziehen konnte.

DAS BÄNDERMODELL:

Um die vielfältigen Effekte und elektrischen Eigenschaften von Leitern und Halbleitern erklären zu können, greift man gerne auf eine Modellvorstellung zurück, in der man die verschiedenen Energiezustände der freien und gebundenen Elektronen eines Elementes hierarchisch übereinander angeordneten (virtuellen) Ebenen (Bändern) zuordnet.-Diese Bänder existieren natürlich nicht wirklich, sondern sind ebenso wie das Bohr'sche Atommodell mit seinen Elektronenschalen nur eine reine Hilfskonstruktion die es unserer menschlichenVorstellungskraft erleichtert,mit den hochkomplexen Vorgängen auf atomarer Ebene umzugehen und zu arbeiten.

Wie wir vielleicht noch entfernt aus dem Physikuntericht der Schule wissen, sind alle Atome wie kleine Sonnensysteme aus einem zentralen positiv geladenen Atomkern aus Protonen (Positive Teilchen) und Neutronen (Neutrale Teilchen) aufgebaut, welcher von negativen Teilchen, den Elektronen umkreist wird.-Diese Elektronen befinden sich immer paarweise in unterschiedlichen "Schalen" um den Kern und jede dieser Schalen kann nur eine bestimmte Zahl von Elektronenpaaren aufnehmen um gesättigt zu werden und dann nach aussen elektrisch neutral zu erscheinen. Von innen nach aussen werden diese Schalen immer größer und bieten dann auch entsprechend mehr Elektronen Platz als die jeweils darunterliegenden. Die genaue Anzahl der Schalen, und damit auch die Anzahl erforderlichen Elektronen eines Elementes hängt von dessen Ordnungszahl im Periodensystem der Elemente ab, also von der Anzahl der Protonen im Kern. In der Praxis haben aber nur Edelgase das Feature, dass Protonen und Elektronen jedes einzelnen Atoms in exact der gleichen Anzahl vorhanden sind, um die bestehenden Schalen um den Atomkern herum genau aufzufüllen.-Diese Edelgase verhalten absolut elektrisch neutral und chemisch sehr verbindungsunwillig (inert) weil gewissermassen ein Idealzustand (Edelgaskonfiguration) vorliegt, der ein Optimum an Stabilität darstellt. Alle anderen Elemente leiden jedoch unter mehr oder weniger großen Elektronendefiziten in ihrer äußersten Schale und sind deshalb gezwungen, sich einzelne Elektronen mit einem oder mehreren Atomen des gleichen oder auch eines fremden Elementes zu teilen um so wieder Elektronenpaare zu bilden und damit die ersehnte Edelgaskonfiguration doch noch zu erreichen.- So kommt es zur Atombindung (Kovalenzbindung) und es entsteht bei diesem Zusammenschluss ein sogenanntes Molekül. Die Anzahl der gemeinsam nutzbaren Elektronenpaare entspricht dabei der Anzahl der möglichen Bindungen.So verbinden sich etwa 2 Stickstoffatome mittels 3 gemeinsamer Elektronenpaare (Dreifachbindung) zu einem Stickstoffmolekül und erreichen damit quasi Edelgasstatus.-Diese kovalente Dreifachbindung ist immerhin so stabil, dass Stickstoff nur sehr schwer weitere chemische Verbindungen eingeht, elektrisch völlig neutral reagiert (Isolator) und in der Praxis als Schutzgas (Inertgas) Verwendung findet. Nun sind aber keineswegs alle Elemente in der glücklichen Lage, stabilen Edelgasstatus zu erreichen. Meist müssen sie sogar selbst noch im Molekülverband schmerzliche Elektronendefizite hinnehmen, was sie chemisch ausserordentlich reaktiv werden lässt und auch für ein völlig anderes elektrisches Verhalten sorgt. Stellen wir uns etwa freie Elektronen in der äußersten Schale vor, so liegt nahe, eine gewisse elektrische Polarisierung zu unterstellen.-Das ist allerdings noch weit entfernt von einer elektrischen Leitfähigkeit, da diese ja den Transport von Elektronen durch ein bestimmtes, atomar oder molekular geordnetes und polares Medium voraussetzt. Diese Ordnung ist in idealer Weise in kristallinen Gitterstrukturen, zum Beispiel von Metallen gegeben. Hier sitzen brav aufgereit nach einem bestimmten Muster Metallatome neben Metallatomen und bilden miteinander ein molekulares Netzwerk aus. Durch die thermische Molekarbewegung jedoch befinden sie sich aber nicht in Ruhe, sondern in einer Art ständiger Vibration und Umschichtung, wodurch sich laufend Elektronen aus den äußersten Schalen lösen und frei im Gitter herumschwirren (Elektronengas).-Diese Elektronen lassen sich natürlich durch externe positive oder negative Ladungen beeinflussen und können das Metallgitter sogar völlig verlassen.-Das Bändermodell beschreibt nun einfach die verschiedenen Energiezustände von Elektronen in solch einem System und ordnet sie bestimmten Energiebändern zu:

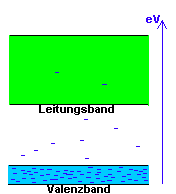
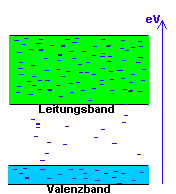
Das unterste Band wird demnach von Elektronen besetzt, die sich noch im Bindungszustand mit dem eigenen oder den benachbarten Atomkernen befinden. Sie sind nicht frei beweglich und stehen somit für einen Ladungstranport auch nicht zur Verfügung.- Dieses Band wird im Modell als VALENZBAND bezeichnet. Energetisch über dem Valenzband befindet sich das sogenannte LEITUNGSBAND, in welchem sich per Definition ausschließlich die freien Elektronen befinden, die aufgrund ihrer Beweglichkeit auch für einen Ladungstransport geeignet sind. Entsprechend diesem Modell befinden sich also bei Metallen durch die thermische Molekularbewegung ständig eine erhebliche Anzahl von Elektronen im Leitungsband. -Das heißt, Metalle sind auch gute elektrische Leiter. Bei Isolatoren dagegen , wie etwa Stickstoff oder den meisten anderen Nichtmetallen befinden sich unter Normaltemperatur fast alle Elektronen im Valenzband und stehen einem Ladungstransport damit auch nicht zur Verfügung.

Isolator+reiner Halbleiter	Metall

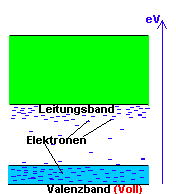
Eine Sonderstellung nehmen nun die Halbleiter ein. Bei reinen Halbleitern befinden sich immer einige, freie Elektronen stark abhängig von der Temperatur weder im Leitungsband noch im Valenzband, sondern normalerweise irgendwo dazwischen.-Das nächsthöhere Leitungsband liegt energetisch mit ca.1eV (=Elektronenvolt) genau soviel höher, dass davon nur wenige Elektronen den Sprung bis ins Leitungsband alleine mittels ihrer thermischen Bewegung schaffen. Der reine Halbleiter verhält sich also bei tiefen Temperaturen zunächst wie ein Isolator. Dies ändert sich dann aber in bestimmten Grenzen bei der Einwirkung externer Energien wie starker Strahlung, Licht, oder Hitze und in dramatischer Weise bei dem Vorhandensein von Fremdatomen mit Elektronenüberschuss (n-Halbleiter) oder Elektronenunterschuss (p-Halbleiter) im Kristallgitter des Halbleiters. Den Vorgang der "Verunreinigung" mit Fremdatomen bezeichnet man als Dotierung.

n-Halbleiter	p-Halbleiter

Reines Germanium besitzt in seiner äußersten Schale 4 Elektronen, die aber im Kristallgitter jeweils zur Bindung an 4 Nachbaratome gebraucht werden und deshalb nicht frei beweglich sind wie die Elektronen in einem leitenden Metall.-Das Leitungsband enthält hier nur sehr wenige Elektronen, die sich alleine aufgrund der Wärmebewegung (Brownsche Molekularbewegung) gelöst haben. Diese Elemente leiten den Strom durch ihren hohen spezifischen Widerstand nur schlecht, und zwar umso schlechter, je reiner sie selbst sind. Ein Kristallstab aus 99.99% hochreinem Germanium etwa verhält sich bei tiefen Temperaturen demnach fast wie ein nichtleitender Isolator.-Das ändert sich aber schlagartig, wenn man den Kristall gezielt mit sehr wenigen, bestimmten Fremdatomen (Z.B.: Arsen oder Indium) dotiert. Dadurch schafft man Gitterfehler in der Kristallstruktur die als sogenannte Elektronenfehlstellen mit Mangel an Elektronen ("Löcher") oder Elektronenüberschuss für eine bestimmte Leitfähigkeit sorgen, die nun um Potenzen über der normalen Eigenleitfähigkeit des reinen Halbleiters liegen.

Fügt man etwa Arsenatome(=Elektronendonatoren) mit 5 freien Aussenlektronen in einer Konzentration von etwa 0.0000001% der Germaniumschmelze zu und zieht daraus einen Kristall, erhält man sogenanntes n-dotiertes Germanium mit einem Elektronenüberschuss im Kristallgitter, wodurch sich abhängig von der Temperatur leicht Elektronen ablösen und sich energetisch immer dicht unter dem Leitungsband aufhalten, auch wenn der Kristall selbst elektrisch neutral bleibt. Die im Gitter eingebauten Arsenatome bleiben nach Verlust ihres jeweils überschüssigen 5. Elektrons (Donatoren) als ortsgebundene, positive Raumladungen (Ionen) zurück. Nun bedarf es natürlich nur noch wenig weiterer Energiezufuhr durch Licht oder Wärme, um diese Elektronen ganz ins Leitungsband zu verschieben und den Halbleiter leitend zu machen.

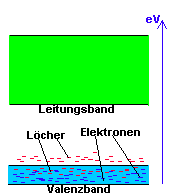
Benutzt man dagegen Indiumatome mit 3 freien Aussenelektronen oder Galliumatome gleicher Konzentration (=Elektronenakzeptoren), schafft man Elektronenmangelstellen, also Löcher oder sogenannte Defektelektronen, die wie bewegliche positive Ladungen wirken, und erhält sogenanntes p-dotiertes Germanium. Auch diese positiven Löcher sind eine Art virtueller,beweglicher Ladungsträger, weil sie sich auf einer energetischen Ebene kurz über dem Valenzband befinden und gewissermassen als "Elektronenfänger" (Akzeptoren) frei durch das Kristallgitter bewegen können.

Entsprechend bezeichnet man die Leitfähigkeit von n(Überschuß)- Halbleitern auch als n-Leitung und analog die Löcherleitung des p(Mangel)- Halbleiters als p-Leitung.

Aber bleiben wir zunächst noch einmal bei dem reinen Halbleiterkristall ohne Dotierung:

Legt man an solch einen Halbleiter eine elektrische Spannung an, so verhält er sich zunächst wie ein normaler, relativ hoher ohmscher Widerstand und so fließt ein stark begrenzter Strom. Dieser Strom steigt allerdings immer weiter an, je heißer der Kristall wird und auch die Einwirkung von Licht führt zu einer erhöhten Leitfähigkeit. In Reihe mit einem Relais oder einer Glühlampe geschaltet kann man so eine einfache Steuervorrichtung aufbauen, die im ersten Falle auf Hitze, und im zweiten Falle auf Licht anspricht. Die so entstandenen Bauelemente bezeichnet man als Heissleiter (NTC) bzw. als Fotowiderstand (LDR). Der prinzipielle Wirkungsmechanismus ist in beiden Fällen ähnlich: Durch Zufuhr äusserer Energie in Form von Wärme oder Licht gerät das Kristallgitter in immer größere Bewegung und es werden Elektronen aus dem Valenzband abgelöst, die dann aufgrund ihres höheren Energiepotentials (Bewegung) ins Leitungsband gelangen. Der Halbleiter erniedrigt seinen spezifischen Widerstand und beginnt immer mehr zu leiten.-Natürlich ist der Zustand bei Entfernung der Wärme- oder Lichtquelle wieder reversibel und die freien Elektronen rekombinieren zurück in ihre Valenzbindungen.-Dies lässt sich beliebig oft wiederholen. Sowohl Heissleiter als auch Fotowiderstand sind äußerlich elektrisch neutral und besitzen keine Gleichrichterwirkung oder Polarisierung.-Sie können also tatsächlich wie reine ohmsche Widerstände behandelt werden und verhalten sich Gleich-und Wechselspannungen gegenüber völlig indifferent.

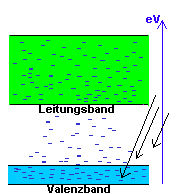Durch Einwirkung von Licht oder Wärme auf einen reinen Halbleiter werden Elektronen ins Leitungsband verschoben

Umgekehrt ist es aber auch möglich, durch Anlegen einer Spannung Wärme zu erzeugen bzw. Licht zu emittieren.-Dies ist aber bei reinen Halbleitern aufgrund des hohen Eigenwiderstandes in der Regel nur mit derart hohen Strömen bzw Spannungen realisierbar,dass der Halbleiter dabei rasch zerstört würde.-In der Praxis verwendet man daher für solche Bauelemente n- und p- dotierte Kristalle, bzw. gleich eine Kombination von beiden als Diode oder Transistor.

Die bevorzugte Nutzung der p- und n- dotierten Halbleiterkristalle aufgrund ihres "aktivierten Zustandes" liegt also auf der Hand.-Verwendet man man bei einem Heissleiter statt reinem Germanium n- dotiertes Germanium, steigern sich die genannten Effekte schon erheblich, da sich bereits viele Elektronen knapp unter dem Leitungsband befinden und somit nur noch wenig externe Energie nötig ist, um eine schon recht brauchbare Leitfähigkeit des Kristalls zu erreichen. Der eigentlicheTrick dabei ist allerdings, dass man in einem einzelnen Kristall zwei oder mehr Zonen mit unterschiedlicher Dotierung ( p und n ) einbaut, so dass sich in der Kristallmitte automatisch Grenzflächenphänomene zwischen p- und n-dotierter Schicht ausbilden, die gewissermassen wie die Metallspitzen der bereits besprochenen Spitzenhalbleiter wirken.